Wer schneller fährt, kommt kaum früher an – der Grenznutzen des Schnellerfahrens

• Systemdenken
• Engineering

Nico Litschke • 18.11.2025 • 8 min

Was halten Sie von diesem Tacho? Ist er nützlich? Wäre das im Auto sinnvoll? 
Ich freue mich auf Ihre Meinung.

Der Rest des Beitrags erläutert die Probleme und Lösungen im Detail.

— Ihr, Nico Litschke

Neulich war ich auf einer Vertriebsfahrt und geriet wegen eines Staus in Zeitdruck. Für 85 km Autobahn, etwas Landstraße und das Parkhaus blieben mir 60 Minuten. Wie schnell sollte ich fahren, um rechtzeitig anzukommen? Baustellen waren mir nicht bekannt, das Navi meldete keine Verzögerungen. Spontan dachte ich: Wenn ich auf der Autobahn entspannte 125 km/h fahre, brauche ich etwa 50 Minuten. Wenn ich 20 % schneller fahre, also rund 150 km/h, müsste ich weitere 20 % Zeit sparen und in etwa 40 Minuten ankommen. Gedacht, gefahren.

Verwirren Sie die Prozentpunkte? Das war mein kleines didaktisches Attentat. Unser Gehirn ist miserabel im Umgang mit Prozenten. Es erwartet eine lineare Welt. Deshalb denke ich spontan: Wenn ich 20 % schneller fahre, bin ich 20 % früher da. Diese Intuition trügt.

Mit kurzem Nachdenken wird klar:

\(v=\frac{\large s}{\large t}\to t=\frac{\large s}{\large v}\)

Die Geschwindigkeit steht im Nenner. Das macht den Zusammenhang nichtlinear. Physikalisch ist das simpel; der Punkt ist: Ich musste bewusst darüber nachdenken. Daniel Kahneman hat diesen Umstand in „Thinking, Fast and Slow“ beschrieben.[1] Unser Denken arbeitet in zwei Modi: 

• schnelles, intuitives Denken wie meine Schätzung 
• langsames, analytisches Denken wie die Schulformel 

Beide gleichzeitig kann das Gehirn nicht. Es muss aktiv umschalten.[2]

Wie viel mehr Output entsteht bei 10 % mehr Input? Wir sind so sehr an solche Fragen gewöhnt, dass wir ihre Tücken oft übersehen. Zwei Beispiele zeigen, warum das ungünstig ist.

Im Streben nach einer Schlagzeile schreibt ein Journalist: „Kaffee senkt das X-Y-Risiko um 10 %.“ Natürlich tut er das nicht. Die Positivrate steigt nur von 10 auf 11 von 100 Personen, also um 1 Prozentpunkt. Gerd Gigerenzer und Kollegen zeigen viele weitere Fälle aus der Diagnostik, in denen sich Menschen teuren und teils schmerzhaften Verfahren unterziehen, obwohl der Nutzen gering ist.[3] Ich kenne das auch aus dem Gym und der Ernährung: In den sozialen Medien herrscht ein Hype um das angeblich effektivste Training und die beste Ernährung, bei dem Prozentpunkte aus Studien zitiert werden. Doch die entscheidende Frage lautet: Wie groß ist der Effekt in absoluten Zahlen? Wenn ich in drei Monaten 10 % mehr abgenommen habe, können das absolut nur etwa 200 g sein. Ein Glas Wasser. Wo ist das relevant, außer im Profisport?

Oder denken wir an Dr. Grey und Dr. House, die mit Chuzpe sagen: „Seine Überlebenswahrscheinlichkeit liegt nur bei 10 %!“ Nein, tut sie nicht. Diese Werte sind Mediane oder Mittelwerte einer Population. Versicherungen kalkulieren so, weil sie Kollektive versichern. Der Staat plant MRT-Stationen nach Bevölkerungsstatistiken. Beim Grippeschutz wird die Bevölkerung geschützt. Ein Arzt sieht jedoch immer den einzelnen Patienten. Dieser liegt selten genau im Mittel. Er ist irgendein Punkt oder ein Ausreißer unter der Glockenkurve. Wie sollte man also an das Risiko herangehen? Man betrachtet es in absoluten Größen. Wie geübt ist der Arzt in dieser Behandlung? Anfang des Jahres ließ ich einen Schlüsselbeinbruch richten. Ich habe mich gegen eine OP durch den Chefarzt und für die Oberärztin entschieden. Warum? Weil sie täglich mehrere ähnliche Fälle versorgt.

Das Preisschild anheften. Die reale Konsequenz zeigt sich immer in absoluten Zahlen — Euro, Liter, Gewicht, Meter, Dauer oder Anzahl.

Trotzdem wird fast überall mit Prozenten hantiert: Rabatte, Steuerbelastung, Renditen, Zinsen, Auslastung, Inflation oder Überlebenswahrscheinlichkeiten. Doch ist klar, 

• dass man bei einem Zinssatz von 3,5 % über 20 Jahre das Haus doppelt abzahlt (\(1,035^{20}\approx 2\))?
• dass 20 % Rabatt auf einen 80-Cent-Artikel 16 Cent sparen? 
• dass bei „40 % Steuerbelastung“ meist der Grenzsteuersatz gemeint ist und man real nur 25 % von 65.000 € = 16.500 € Steuern zahlt?[4]
• dass bei „10 % Sterblichkeit“ die reale Betroffenheit fehlt, etwa 10 % von 2 von 100 betroffenen Personen?

Prozentangaben verschleiern die reale Konsequenz. Übersetzen Sie Prozente deshalb immer in absolute Zahlen.

Wie schnell sollten wir nun fahren? Solche Fragen lassen sich nicht rational beantworten. Wenn ich ein Snickers essen möchte, nehme ich das Angebot mit 20 % Rabatt für 64 Cent statt des Normalpreises von 80 Cent. Egal, worum es geht: Wenn wir etwas wertschätzen, bevorzugen wir mehr davon – oder besser, früher, günstiger, rentabler. Eine Grenze gibt es dabei nicht, und damit auch kein Entscheidungskriterium.

In der Wert- und Entscheidungstheorie gilt der abnehmende Grenznutzen als anerkannte Grundlage.[5] Statt der Gesamtmenge betrachten wir die nächste Einheit und den Nutzen, den sie stiftet. Wer eine Stunde Sport pro Woche treibt statt gar keinen, darf einen großen Vorteil für die Gesundheit erwarten. Wer dagegen 11 statt 10 Stunden trainiert, sollte keinen großen Zusatznutzen erwarten.

Der abnehmende Grenznutzen lässt sich auf fast alles anwenden. So auch auf die Ausgangsfrage des Schnellfahrens: Je schneller wir fahren, desto früher kommen wir an. Klar. Als Grenznutzen formuliert: Wie viel Zeit spart man, wenn man 10 km/h schneller fährt?

Zunächst legen wir die Strecke auf eine einheitliche Bezugsgröße fest. Ich wähle s = 100 km, da diese Strecke bei uns üblich ist. Diese setzen wir in die bekannte Formel ein:

\(t=\frac{\large 100\ km}{\large v}\)

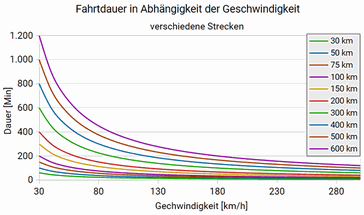
Die folgende Grafik zeigt, wie lange man bei unterschiedlichen Geschwindigkeiten für diese Strecke benötigt:

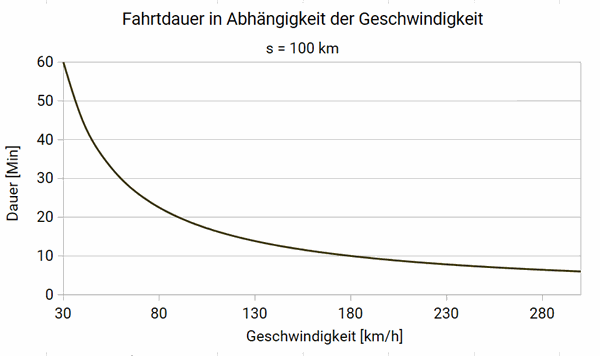
Der abnehmende Grenznutzen ist deutlich erkennbar. Mit höherer Geschwindigkeit schafft man die Strecke zwar schneller, aber nicht im gleichen Maß. Ein Extrembeispiel: Mit 300 km/h ist man nur halb so lange unterwegs wie mit 200 km/h, spart aber nur zehn Minuten. Hier liegt das Kontraintuitive: Erst die absoluten Zahlen verdeutlichen die realen Konsequenzen.

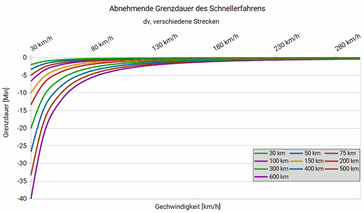
\(t'(v)=\frac{\large dt(v)}{\large dv}=-\frac{\large 100\ km}{\large v^2}\)

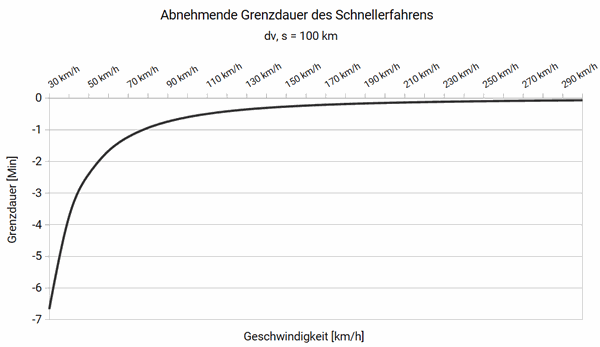
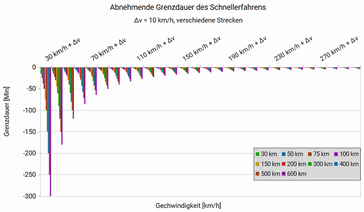
Diese Darstellung ist formal korrekt, für die Praxis jedoch sperrig. Der Anstieg zeigt den minimalen Grenznutzen bei minimal höherer Geschwindigkeit. Daraus lässt sich nicht direkt ablesen, wie viel schneller man tatsächlich ist. Deshalb wähle ich eine praktisch relevante Differenz von Δv = 10 km/h:

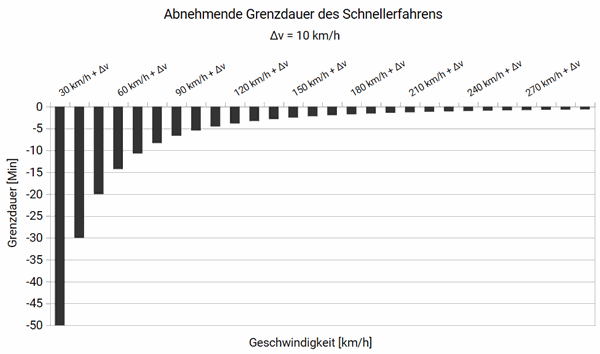
Die Grafik zeigt den Grenznutzen eindeutig: Wer bei 100 km/h um 10 km/h beschleunigt, spart auf 100 km rund 5:30 Minuten.

Wir müssen nicht bei einer Strecke von 100 km bleiben. Jede andere Strecke funktioniert genauso, etwa der Arbeitsweg oder die Heimreise. In der Formel wirkt die Strecke nur als Faktor und streckt oder staucht die Kurven:

Allerdings sind diese Grafiken an sich für viele Menschen nicht intuitiv lesbar und taugen nicht im Alltag.

Bei vielen technischen Anwendungen müssen wir die Mensch-Maschine-Schnittstelle per Design absichern. Beispiele sind der Zugang zu gefährlichen Maschinen, die richtige Ausrichtung von Steckern, das Starten des Autos durch zwei Interaktionen (etwa Bremse und Zündung) oder Spezialschrauben, die Hobbybastler von gefährlichen Teilen fernhalten. All das sind „Poka-Yoke“-Mechanismen, die den Umgang des Menschen mit Technik absichern.

In diesem Sinne fassen wir die vorherigen Überlegungen zusammen: Der Grenznutzen des Schnellerfahrens, gemessen in absoluter Zeit, muss beim Fahren ohne Nachdenken verfügbar sein. Deshalb habe ich den klassischen Tacho um die blaue Kurve ergänzt. Sie ist eine einfache, aber zutreffende Entscheidungsregel[6] und zeigt, wie lange man für 100 km bei der aktuellen Geschwindigkeit benötigt:

Den Grenznutzen aus Grafik 3 habe ich bewusst weggelassen. Größere Geschwindigkeitssprünge erfordern mehr Nachdenken – und genau das wollen wir hier vermeiden. So bleibt der Zusammenhang gut lesbar. Beschleunigt man etwa von 80 km/h auf 130 km/h, benötigt man 46 Minuten statt 1:15 h, also 30 Minuten weniger. Trotz aller Formeln und Grafiken ist diese Darstellung für mich am einprägsamsten. 

Der Charme des Grenznutzens liegt in seiner Einfachheit. Ein paar Minuten früher anzukommen, macht oft keinen Unterschied. Das leuchtet unmittelbar ein. Bei Rettungs- und Feuerwehrfahrten gilt das allerdings nicht.

Wir brauchen dafür auch keine Kriterien, die mehr Daten, mehr Rechenarbeit und mehr Streit erzeugen, etwa zu Energieverbrauch, CO₂-Ausstoß oder zur Gefährdung anderer. Solche Debatten enden schnell in ideologischen Etiketten. Der Grenznutzen umgeht das. Er ist eine einfache, unstrittige physikalisch-ökonomische Aussage.

Spannend werden die Bereiche mit hohem Grenznutzen. Ein 40-Tonner, der 80 km/h statt 60 km/h fährt, spart 25 Minuten auf 100 km. Das ist ein klarer Anreiz zum Schnellfahren. Umgekehrt ist der Grenzschaden groß, wenn die Geschwindigkeitsbegrenzung in Innenstädten von 50 km/h auf 30 km/h sinkt. Pro Person gehen 1:20 h auf 100 km verloren.

Das sind jedoch großpolitische Themen. Für den Alltag reicht eine einfache Orientierungshilfe. Damit Entscheidungen beim Fahren rational und leichtfallen, ist dieser Tacho ein niederschwelliges Hilfsmittel.

— Ihr, Nico Litschke

1. ↑ Kahneman, D. (2011). Thinking, fast and slow. New York: Macmillan.
2. ↑ Oakley, B. A. (2014). A mind for numbers. New York: Jeremy P. Tarcher/Penguin.
3. ↑ Gigerenzer, G. (2008). Bauchentscheidungen. Die Intelligenz des Unbewussten und die Macht der Intuition (Vol. 1). München: Goldmann.
4. ↑ Im Internet: https://www.bmf-steuerrechner.de/ekst/eingabeformekst.xhtml
5. ↑ Menger, C. (1871). Grundsätze der Volkswirtschaftslehre. Erster Allgemeiner Teil. Wien: Braumüller.
6. ↑ Gigerenzer, G., & Gaissmaier, W. (2011). Heuristic decision making. Annual Review of Psychology, 62, 451–482. https://doi.org/10.1146/annurev-psych-120709-145346