Droge Varietät: Vernetzter, intelligenter, leistungsfähiger?

Ein fast intuitiver Zugang zu Komplexität liegt in der möglichen Vielfalt („Varietät“) eines Systems. Malik definiert:[1]

Genau genommen, können wir diese Varietät nur rechnerisch schätzen:

• die Anzahl der Knoten \(n\)
• die Anzahl und Art der Kanten \(k\)
• ihren Graph \(g\)
• und den Zustand \(z\) der Kanten

Spontan klingt das plausibel: Je mehr Teile interagieren, desto komplexer wirkt das System. Das, so erklärt Malik, sei ein „»Rohstoff«, eine neue Form von Kapital“, durch den „... Organisationen leistungsfähiger, effektiver, schneller, flexibler und intelligenter“ würden.[1]

Leistungsfähigkeit und Intelligenz hänge unmittelbar von der Komplexität eines Systems ab:

Ein Grund, genauer hinzusehen. Das Konzept der Varietät verdeutlichen wir an folgendem Beispiel: Als ich meinen Audi kaufte, war CarPlay nicht verfügbar. Erst ein zusätzliches Steuergerät (ECU) machte es möglich. Seit der Vernetzung kann ich über das Auto auf Connectivity-Dienste wie Karten, Blitzer-App, Audible oder Nachrichten zugreifen:

Das vernetzte Auto lässt sich als Graph darstellen. Teilsysteme sind Knoten, Schnittstellen Kanten:

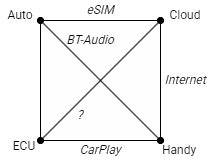
Durchzählen ergibt:

\( n = 4 \)

\( k = \frac{n(n-1)}{2} = \frac{4 \cdot 3}{2} = 6 \)

Da die mit dem Fragezeichen versehene Schnittstelle real fehlt, sind es tatsächlich \(k=5\) Kanten. Zum Vergleich: Ein System mit \(n=12\) Knoten hätte bereits \( k = 66 \) Kanten:

In manchen Kontexten sind Kanten gerichtet, z.B. Paul liebt Karla, Karla aber nicht Paul. Dann gilt:

\( k = n(n-1) \)

Doch meine Connectivity-Lösung war unelegant. Lieber wäre mir:

Diese Lösung hat gerignere Varietät bei gleicher Leistungsfähigkeit. Mehr noch: Sie ist robuster, also weniger fehleranfällig. In meiner realen Lösung mit \( k = 5 \) Schnittstellen kann jede „gut“ oder „schlecht“ funktionieren. Das sind mindestens \( m = 2 \) Zustände pro Kante. Damit gibt es 

\( z \geq m^k = 2^5 = 32 \)

mögliche Systemzustände. Nur in 2 Zuständen funktioniert Connectivity; in mindestens 30 ist sie defekt. Folgende Automatentabelle zeigt das anschaulich:

Fazit: Höhere Varietät bringt mehr Leistungsfähigkeit, aber auch Fehlerzustände. Ein eleganteres Design mit geringerer Varietät erreicht die gleiche Leistungsfähigkeit und ist gleichzeitig robuster. Ein Widerspruch?

Der scheinbare Widerspruch geht auf eine Grundlage der Komplexitätstheorie zurück. Ashby leitete anhand von Logiktabellen das „Gesetz der erforderlichen Varietät“ her:[2]

Ein System kann seine Funktion nur dann verlässlich ausführen, wenn es alle auftretenden Störungen erkennen und behandeln kann. Folglich muss die Varietät \(\mathbb{V}\) des Systems mindestens so hoch sein wie die der Störungen:

\( \mathbb{V}_{System} \geq \mathbb{V}_{Störungen} \)

Doch in der Praxis liegt die Störungsvielfalt meist weit über dem theoretischen Minimum:

\( \mathbb{V}_{System} \;\geq\; \mathbb{V}_{Störungen} \;{\color{red}{\boldsymbol{>}}}\; m^k \;=\; m^{\left(\tfrac{n(n-1)}{2}\right)} \)

Selbst bei der eleganteren Lösung mit direkter Internetverbindung ohne ECU und Handy finden wir deutlich mehr als \( m = 2 \) mögliche Zustände. Das Problem: Wir wissen nicht, wie viele es tatsächlich sind. Meist erfahren wir es nur durch Trial & Error. Selbst dann bleibt: Fehlerfreiheit ist nicht beweisbar.[3] Deshalb lassen Safetynormen wie ISO26262[4] oder IEC61508[5] auch für sicherheitskritische Systeme eine Restfehlerspanne zu.

Hinzu kommt: Die Requisite Variety betrachtet nur Funktionalität. Für reale Systemlösungen zählen z. B. auch Performance, Safety, Security, Verlustleistung, Kühlung, Größe, Updatefähigkeit, Isolation und Kosten. Das sind keine Störungen, aber entscheidungsrelevant.

Penzlin beschreibt analog für die Natur: Kombinatorisch lassen sich unzählige DNA-Basenfolgen bestimmen. Davon ist nur ein winziger Bruchteil stabil und überlebensfähig, z. B. wegen Energie- oder Ressourcenverbrauch.[6]

Fazit: (Erforderliche) Varietät ist weder ein objektives Maß noch praxistauglich. Sie hängt von der gewählten Bezugsebene des Beobachters ab. Damit sagt sie eher etwas über den Beobachter aus und nicht über das System. Als „Gesetz“ ist es dann doch etwas hochgegriffen.

Im Alltag begegnen uns viele kombinatorische Optimierungsprobleme. Beispiel: Bei einem Fehler meiner Connectivity-Lösung stellt sich die Frage: In welcher Analysereihenfolge finde ich am schnellsten die Ursache? Bei \(k=5\) Schnittstellen gibt es 

\( 5! = 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 120 \)

mögliche Reihenfolgen. Berücksichtige ich die \( z \geq 32 \) Zustände, explodiert die Zahl:

\( 32! = 2{,}63 \cdot 10^{35} \)

Plot Twist: Es ist fast immer Bluetooth. Sinnvoller als die Permutation ist die Fehlersuche über Verteilungen wie die 80-20-Regel[7] oder die Weibullverteilung[8] einzugrenzen.

Ähnliche Heuristiken nutzen wir in der Kryptographie, Rundreisen (Travelling Salesman[9]) , Knapsack-Problem[10], Produktionsplanung (lineare Optimierung[11]). Und als Schweizer Taschenmesser: „evolutionäre Algorithmen“.[12]

Fazit: Für kombinatorische Optimierungsprobleme ist die Idee der (erforderlichen) Varietät irrelevant. Sie beeinflusst nicht die Funktionsweise der eingesetzten Heuristiken.

Glaubt man dem LinkedIn-Mainstream der Organisationsberatung, dann steckt in der Varietät ein Heilsversprechen: Man müsse Organisationen nur besser – intelligenter – vernetzen, schon steige ihre Leistungsfähigkeit.[13] Das dezentrale, selbstorganisierte Team wird zur Allzwecklösung stilisiert; die Hierarchie zum Übel, das es zu bewältigen gilt.

Das ist eine unhaltbare Vereinfachung. Dezentralisierung bringt auch Dysfunktionen: weniger Stetigkeit, unklare Zuständigkeiten, zähere Entscheidungen[14] – vor allem, wenn unvereinbare Zielkonflikte und „interne Empfindlichkeiten“ berührt werden.[15] Auch das gehört zur Wahrheit.

Die Synthese: föderale Ansätze. Autonome Einheiten kümmern sich um die Belange vor Ort; die Hierarchie koordiniert zwischen ihnen. Systemtheoretisch verkompliziert, findet sich dieser Mittelweg im „Viable System Model“.[16]

Analog zu biologischen und technischen Systemen gilt auch für Organisationen: Leistungsfähigkeit ist nicht allein Frage der Permutationen oder Varietät.

Varietät bringe mehr Intelligenz und Kreativität. Das Gehirn mit seinen 100 Billionen Synapsen gilt als Paradebeispiel. Doch Intelligenz beruht nicht allein auf der Menge an Verbindungen, sondern auf selbstorganisierter Musterbildung („Autopoiesis“[17] und „Neuroplastizität“). Sonst wäre ein Wassertropfen mit Milliarden Wassermolekülen auch intelligent.

„Viele Köche verderben den Brei“ bringt es auf den Punkt: Ein kleines, schlagkräftiges Projektteam kann oft mehr leisten als ein großes; schlicht, weil der Koordinationsaufwand sinkt.

Noch schlagkräftiger ist der Großmeister (Stichwort: Shu Ha Ri[18]), der im Alleingang ein ganzes Team ersetzen kann. Nur sind Normalos wie ich auf einen kleinen Kompetenzbereich spezialisiert. Vernetzung ist daher eine praktische Notwendigkeit. 

Varietät ergibt sich aus dieser Arbeitsteilung; sie ist weder notwendige noch hinreichende Bedingung für Intelligenz und Kreativität in Organisationen.

Herkömmliche Teamarbeit, Meetings, Konferenzen sind für Hochleistung angeblich untauglich. Zu schwach. Zu langsam. Zu viel Menscheln. Stattdessen, so versichern uns Berater, müsse die Varietät der Organisation hochgekurbelt werden.[19]

Die Lösung: Workshops, die optimal – was sonst – mittels Graphen organisiert werden. Themen sind Knoten, Menschen sind Kanten. Je nach Graph entstehen verschiedene Workshopdesigns. Beispiele mit \(n=12\) Themen:

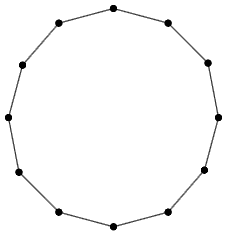
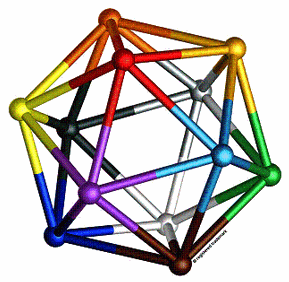
Die Vernetzung des Graphen bestimmt, wie viele Personen parallel an welchen Themen arbeiten können.

Besonders optimal: platonische Körper wie der Ikosaeder.[20] Sie sollen die Distanz zwischen Personen und Themen minimieren.[21] Methodisch heißt das: geometrische Symmetrieeigenschaften werden auf soziale Vorgänge übertragen. Das ist, als würde man eine Beobachtung aus dem Chemiebaukasten direkt auf den menschlichen Organismus extrapolieren. Nicht sauber, klingt aber mathematisch präzise – und bei Weitem ansehnlicher als 2D-Graphen.

Workshops gehören zweifellos zum Repertoire des Problemlösens. Nur: Ob die Wirksamkeit aus optimalen Graphen stammt oder schlicht daher, dass Experten endlich Zeit und Fokus für ein gemeinsames Thema haben, ist bislang nicht untersucht. Ich tippe eher auf Letzteres.

Im Artikel über VUCA, Cynefin & Co. zeigte ich auf, warum Vierfeldermatizen keine Orientierung in einer komplexen Welt geben. Auch die Requisite Variety wurde in eine Matrix gepresst, und willkürlich in „einfach“, „komplex“ und „chaotisch“ segmentiert:[23]

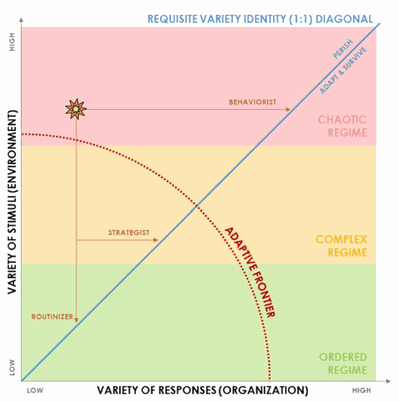
Tatsächlich müssten die Achsen logarithmisch skaliert sein, weil Permutationen deutlich schneller als exponentiell wachsen. Mit korrekter Skalierung verschwinden die hübschen Geraden und Kreisausschnitte.

So wird uns eine „Theorie“ vorgegaukelt. Genau der Szientismus, den Nassim Taleb kritisiert.[24] Ich schließe mich dem an.

Ausgangspunkt war die Hypothese, die Leistungsfähigkeit eines Systems sei proportional zu dessen (erforderlicher) Varietät. In technischen, biologischen, sozialen, heuristischen, kognitiven und kollaborativen Bereichen ist sie zu verwerfen. Am Ende bleiben nur die mahnenden Worte Norbert Wieners:

— Ihr, Nico Litschke

1. ↑ Malik, F. (2015). Navigieren in Zeiten des Umbruchs: Die Welt neu denken und gestalten (1. Aufl., S. 44). Frankfurt/New York: Campus Verlag.
2. ↑ Ashby, W. R. (1961). An introduction to cybernetics (4th impr.). London: Chapman & Hall.
3. ↑ Dijkstra, E. W. (1972). The humble programmer. Communications of the ACM, 15(10), 859–866. https://doi.org/10.1145/355604.361591
4. ↑ ISO 26262-5:2018. (2018). Road vehicles — Functional safety — Part 5: Product development at the hardware level (2nd ed.). International Organization for Standardization.
5. ↑ IEC 61508. (2010). Functional safety of electrical/electronic/programmable electronic safety-related systems. International Electrotechnical Commission.
6. ↑ Penzlin, H. (2016). Das Phänomen Leben: Grundfragen der Theoretischen Biologie (S. 305f.). Springer Berlin Heidelberg. https://doi.org/10.1007/978-3-662-48128-8
7. ↑ Wikipedia. (2025). Paretoprinzip. In Wikipedia – Die freie Enzyklopädie. Abgerufen am 17.08.2025 von https://de.wikipedia.org/w/index.php?title=Paretoprinzip&oldid=258797128
8. ↑ Wikipedia. (2025). Weibull-Verteilung. In Wikipedia – Die freie Enzyklopädie. Abgerufen am 17.08.1985 von https://de.wikipedia.org/w/index.php?title=Weibull-Verteilung&oldid=257468721
9. ↑ Wikipedia. (2025). Problem des Handlungsreisenden. In Wikipedia – Die freie Enzyklopädie. Abgerufen am 18.08.2025 von https://de.wikipedia.org/w/index.php?title=Problem_des_Handlungsreisenden&oldid=252524720
10. ↑ Wikipedia. (2025). Rucksackproblem. In Wikipedia – Die freie Enzyklopädie. Abgerufen am 18.08.2025 von https://de.wikipedia.org/w/index.php?title=Rucksackproblem&oldid=252301004
11. ↑ Wikipedia. (2025). Lineare Optimierung. In Wikipedia – Die freie Enzyklopädie. Abgerufen am 18.08.2025 von https://de.wikipedia.org/w/index.php?title=Lineare_Optimierung&oldid=256915613
12. ↑ Wikipedia. (2025). Evolutionärer Algorithmus. In Wikipedia – Die freie Enzyklopädie. Abgerufen am 18.08.2025 von https://de.wikipedia.org/w/index.php?title=Evolution%C3%A4rer_Algorithmus&oldid=257549584
13. ↑ Malik, F. (2015). Navigieren in Zeiten des Umbruchs: Die Welt neu denken und gestalten (1. Aufl., Kap. 5). Frankfurt/New York: Campus Verlag.
14. ↑ Luhmann, N. (1991). Soziale Systeme: Grundriss einer allgemeinen Theorie (4. Aufl.). Frankfurt am Main: Suhrkamp.
15. ↑ Kühl, S. (2011). Organisationen: Eine sehr kurze Einführung (1. Aufl., S. 71). Wiesbaden: Springer VS.
16. ↑ Beer, S. (2004). Diagnosing the system for organizations. Chichester: John Wiley & Sons.
17. ↑ Maturana, H. R., & Varela, F. J. (1991). Autopoiesis and cognition: The realization of the living. Dordrecht: Springer Netherlands.
18. ↑ Wikipedia. (2025). Shuhari. In Wikipedia – The Free Encyclopedia. Retrieved 17.08.2025 from https://en.wikipedia.org/w/index.php?title=Shuhari&oldid=1303951898
19. ↑ Malik, F. (2024). Malik Syntegrations-Methodik. Im Internet, Stand: 12.08.2025: https://www.malik-management.com/wp-content/uploads/2024/05/Malik-Syntegration-InfoSheet.pdf
20. ↑ Nittbaur, G. (2005). Stafford Beer's syntegration as a renascence of the ancient Greek agora in present-day organizations. Journal of Universal Knowledge Management, 1, 59–66.
21. ↑ YouTube. (2025). [Video: Vortrag zu Syntegration]. Abgerufen am 18.08.2025 von https://youtu.be/TmoT8Zv4cQg?si=1Faz92M73A-1omgB&t=275
22. ↑ Wiener, N. (2019). Cybernetics: Or, control and communication in the animal and the machine (2nd ed.). Cambridge, MA: MIT Press.
23. ↑ Chester, M. V., & Allenby, B. (2022). Infrastructure autopoiesis: Requisite variety to engage complexity. Environmental Research: Infrastructure and Sustainability, 2(1), 012001. https://doi.org/10.1088/2634-4505/ac48ef
24. ↑ Taleb, N. N. (2018). Skin in the Game. Das Risiko und sein Preis (1st ed.). München: Penguin.