Systemkomplexität reduzieren und auf Ziele optimieren: Fallbeispiel „Vermögensaufbau“

• Systemdenken
• Engineering

DE | EN

Systemverhalten wird an Zielen bemessen, die jedoch häufig widersprüchlich zueinander sind. So steht die Leistungsfähigkeit eines elektrischen Antriebs („Freude am Fahren“) im Spannungsfeld zu Safety, Lebensdauer und Verbrauch. Zudem sind zahlreiche Fachbereiche an der Entwicklung beteiligt. Das Gesamtsystem lässt sich als multidimensionales, nichtlineares Optimierungsproblem beschreiben. Systems Engineering (SE) muss hierfür nicht nur die organisatorische Klammer bilden, sondern auch geeignete Analysewerkzeuge bereitstellen. Dieser Beitrag zeigt, wie sich die Werkzeuge Multidisziplinäre Design Optimierung (MDO), Isoperformance-Analyse (IPA) und Monte-Carlo-Simulation (MC) kombinieren lassen, um ein solches System strukturiert zu optimieren. Die Anwendung wird am Beispiel des komplexen, vernetzten Systems „Vermögensaufbau“ demonstriert. Ergebnis ist eine Komplexitätsreduktion, durch die das ursprüngliche Optimierungsproblem auf ein einfaches Kriterium zurückgeführt wird. 

Mein Geschäft betreibe ich über eine Holding. Ich bin ihr Gesellschafter, sie ist Gesellschafterin des Geschäfts. Umsätze aus dem Geschäft zahle ich mir teilweise als Gehalt aus. Der verbleibende Gewinn wird in der Holding thesauriert. Zusätzlich halte ich Anlagevermögen (AV) in Wertpapieren und Immobilien (VuV). Mit den Geldzuflüssen (Cashflow, CF) aus allen Teilsystemen decke ich meine Lebenshaltungskosten. Das nachfolgende Bild 1 fasst den Systemkontext zusammen:

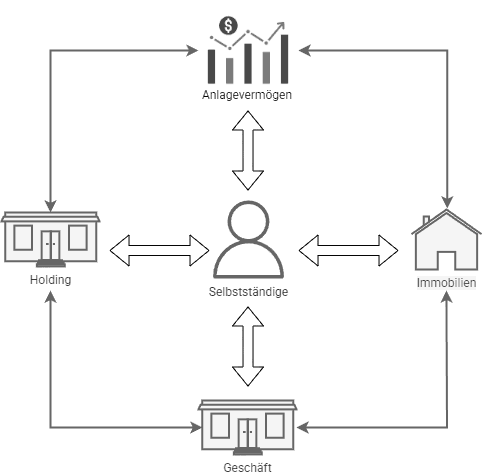
Das System besteht aus vernetzten Teilsystemen mit jeweils eigenen operativen, rechtlichen und steuerlichen Regimen. Gehalt muss ich privat versteuern und mindert gleichzeitig den Gewinn des Geschäfts sowie die Thesaurierung. Theoretisch kann der notwendige Cashflow aus Gehalt, aus der Holding, aus VuV oder aus einer Mischung dieser Quellen stammen. An vielen Stellhebeln lässt sich gleichzeitig drehen – doch welche sind im Gesamtsystem tatsächlich wirksam?

Im Folgenden werden verschiedene Analyseschritte durchlaufen, die zeigen, wie eine solche Optimierung methodisch angegangen werden kann. Auch wenn die Darstellung sequenziell erfolgt, handelt es sich um ein iteratives Vorgehen: Erkenntnisse aus einer Teilanalyse fließen in andere zurück. Ausgangspunkt ist stets eine klare Definition des nichtlinearen Optimierungsproblems (NLP) sowie der zugrunde liegenden Ziele.

Aktuell strebe ich Vermögensaufbau an. Bargeld benötige ich zur Deckung meiner Lebenshaltungskosten. Das ist wichtig zum Verständnis: Meine Lebenshaltungskosten unterliegen keiner „Lifestyle Inflation“. Ich kaufe mir also kein teureres Auto oder eine Luxusreise, nur weil ich es mir leisten kann. Gleichzeitig muss ich streng darauf achten, dass die Teilsysteme liquide bleiben; eine Insolvenz ist unbedingt zu vermeiden. Diese Risiken federe ich durch Liquiditätspuffer ab, die ich „Notgroschen“ nenne. Das zugehörige NLP lautet:

NB1 bis NB3 besagen, dass der jeweilige Notgroschen nicht unter einen Schwellwert fallen soll. Praktisch heißt das: Ich halte stets so viel Geld auf dem Tagesgeld vor, dass ich daraus die Kosten für einen festgelegten Zeitraum begleichen kann, selbst wenn Einkommen und Umsatz vollständig wegfallen. Das beschreibt meine individuelle Risikoaversion; andere Lebensumstände würden andere Schwellwerte erfordern. Durch NB4 werden die Notgroschen idealerweise nicht angetastet. NB5 richtet sich explizit gegen Lifestyle Inflation. RB1 soll einmal investiertes Kapital schützen; „Buy and Hold Forever“ gilt bekanntlich als langfristig optimale Anlagestrategie.

Wichtig: Ziele beschreiben den gewünschten Systemzustand. Kosten, Termine, Safety, Security, Qualität und ähnliche Größen sind in der Regel Neben- oder Randbedingungen, nicht Ziele. Klarheit in dieser Trennung ist Voraussetzung für jede sinnvolle Optimierung.

Wichtig ist auch: Jede Änderung hat Neben- und Fernwirkungen. Was soll sich nicht ändern? Häufig wird übersehen, was aktuell unauffällig ist, aber dennoch wesentlich bleibt.[1]

Im nächsten Schritt überführen wir die Ausgangslage und das NLP in eine MDO-Sicht.

Das nachfolgende Bild 2 überführt den Systemkontext des zugrunde liegenden NLP in eine MDO-Sicht.

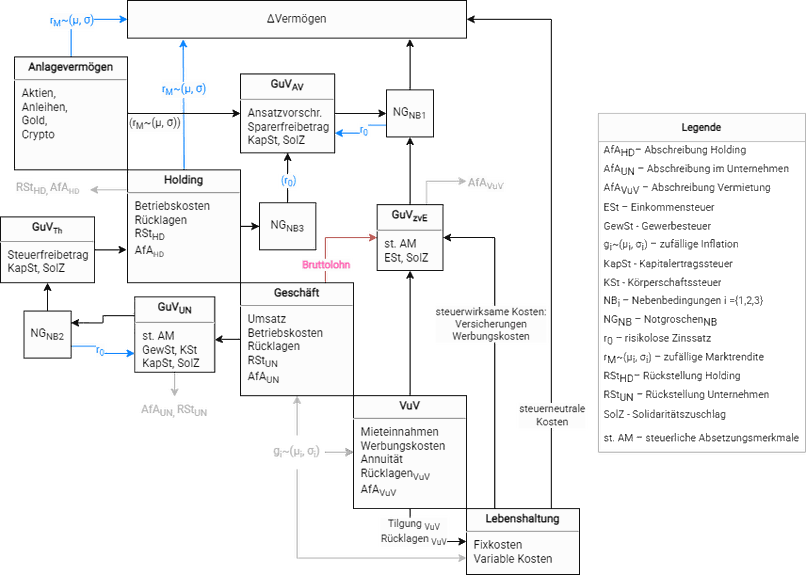
Dargestellt sind die verschiedenen Teilsysteme und ihre Schnittstellen. NB1 bis NB3 sind als Pufferelemente modelliert. NB4 ist dadurch realisiert, dass die Lebenshaltung keinen direkten Eingang aus Einkommensquellen hat. Das Zusammenwirken von versteuertem Einkommen und Lebenshaltungskosten ist im ΔVermögen abgebildet. Einige dieser Kosten wirken sich zugleich auf die Steuerlast aus. Ebenfalls dargestellt ist, dass in der steuerlichen Berechnung fiktive Kosten wie Abschreibungen und Rückstellungen berücksichtigt werden; sie wirken sich rechnerisch aus, führen jedoch nicht zu einem Liquiditätsabfluss und werden daher nach der Versteuerung wieder eliminiert.

Für die weitere Analyse sind insbesondere folgende Variablen ausschlaggebend:[2]

•     Kopplungsvariablen, die Rückkopplungen zwischen den Teilsystemen abbilden.
•     Lokale Variablen, die innerhalb der Teilsysteme zur Transformation von Input in Output erforderlich sind.

In der Praxis identifiziert das SE die Kopplungsvariablen und entwickelt daraus eine MDO-Sicht wie in Bild 2. Die Fachbereiche verantworten ihre lokalen Variablen. Die Kopplungsvariablen strukturieren und vereinfachen damit auch die Kommunikation.

Die Abbildung verdeutlicht die hohe strukturelle und dynamische Kopplung des Systems. Eine exakte Lösung des Ziels unter Einhaltung der NB und RB ist daher kaum praktikabel. Es wäre wenig sinnvoll, Steuerformeln, Gewinnrechnung und Thesaurierung vollständig analytisch zu verknüpfen. Spätestens bei der Modellierung der Liquiditätspuffer müssten zeitabhängige, gekoppelte Gleichungen formuliert und optimiert werden. Zudem wollen wir keine unsachlichen Vereinfachungen annehmen: Künftige Lebenshaltungskosten, Umsätze und Marktrenditen sind unsicher und schwanken zufällig.

Halten wir fest: Anstatt „alles mit allem“ zu verknüpfen, zeigt die MDO-Sicht klar abgegrenzte Systemteile, ausgewählte Schnittstellen und lokale Parameter. Dadurch ist die Komplexität bereits reduziert. Eine exakte Lösung des resultierenden MDO bleibt hier jedoch praktisch nicht erreichbar.

Es braucht eine weitere Reduktion der Komplexität.

Die MDO-Sicht reduziert zwar die strukturelle Komplexität des Systems, lässt jedoch eine hohe kombinatorische Vielfalt möglicher Lösungen zu. Zur weiteren Reduktion dieser Vielfalt wird daher eine Isoperformance-Analyse eingesetzt.

Ziel der IPA ist, Kopplungsvariablen zu identifizieren, die für die Optimierung eine geringe Sensitivität gegenüber anderen Teilsystemen oder dem Systemziel aufweisen und deshalb fixiert werden können.[3]

Eine dieser Variablen sind die Lebenshaltungskosten. Sie unterliegen keiner Lifestyle Inflation, sind nach unten durch Fixkosten begrenzt und wachsen nach oben nicht beliebig. Sie bewegen sich in einem relativ engen Bereich und können daher auf ein konstantes Leistungsniveau („Iso“) fixiert werden.

Auch buchhalterische Gewinne und Verluste des Anlagevermögens und der Holding werden für die Optimierung fixiert, jedoch auf „Null“ und aus einem anderen Grund. Sie können stark schwanken, beruhen auf exogenen Marktentwicklungen und entziehen sich einer gezielten Kontrolle. Entsprechend eignen sie sich nicht zur Optimierung. Gleiches gilt für Gewinn- und Steuerrechnungen, die verbindlichen gesetzlichen Vorgaben folgen und nicht frei gestaltbar sind.

Ein Blick auf die MDO-Sicht zeigt damit: Als nicht fixierte Kopplungsvariablen verbleiben im Wesentlichen Umsatz und Gehalt. Dadurch vereinfacht sich die Optimierungsfrage erheblich: Welche Umsatz-Gehalts-Kombination ist für den Vermögenszuwachs geeignet, um die Lebenshaltungskosten zu decken (NB4)?

Diese starke Vereinfachung ist dem betrachteten System geschuldet. In technischen Systemen verbleibt typischerweise eine größere Anzahl nicht fixierter Kopplungsvariablen.

Die IPA reduziert die kombinatorische Vielfalt, indem für ausgewählte Variablen ein zufriedenstellendes Leistungsniveau festgelegt wird.

Dennoch bleibt das Problem der vernetzten Teilsysteme mit ihren jeweiligen Rechenlogiken und Steuerregimen bestehen. Dieses adressieren wir im nächsten Schritt mit dem Schweizer Taschenmesser der quantitativen Analyse.

Das verbleibende Optimierungsproblem wird in eine MC überführt und statistisch ausgewertet, um den Aufwand einer exakten analytischen Lösung zu vermeiden. Die MC simuliert unterschiedliche Umsatz-Gehalts-Kosten-Kombinationen und ihre Auswirkungen auf den Netto-CF. Das Ergebnis zeigt der 3D-Plot in Bild 3.

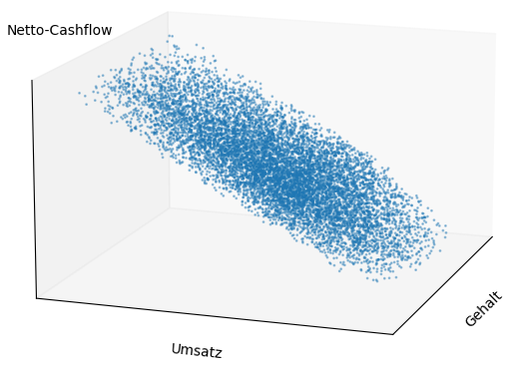
Bemerkenswert ist, was das Bild 3 nicht zeigt: In der schiefen Ebene gibt es weder Tal noch Gipfel oder Sattelpunkt. Zudem verläuft die Ebene nahezu parallel zur Gehaltsachse. In der Projektion auf Umsatz und Netto-CF (Bild 4) zeigt sich, dass das Gehalt nur einen vernachlässigbaren Einfluss hat. Der Netto-CF schwankt lediglich marginal und wird gemäß Regression nahezu vollständig (R² ≈ 99 %) durch den Umsatz erklärt. 

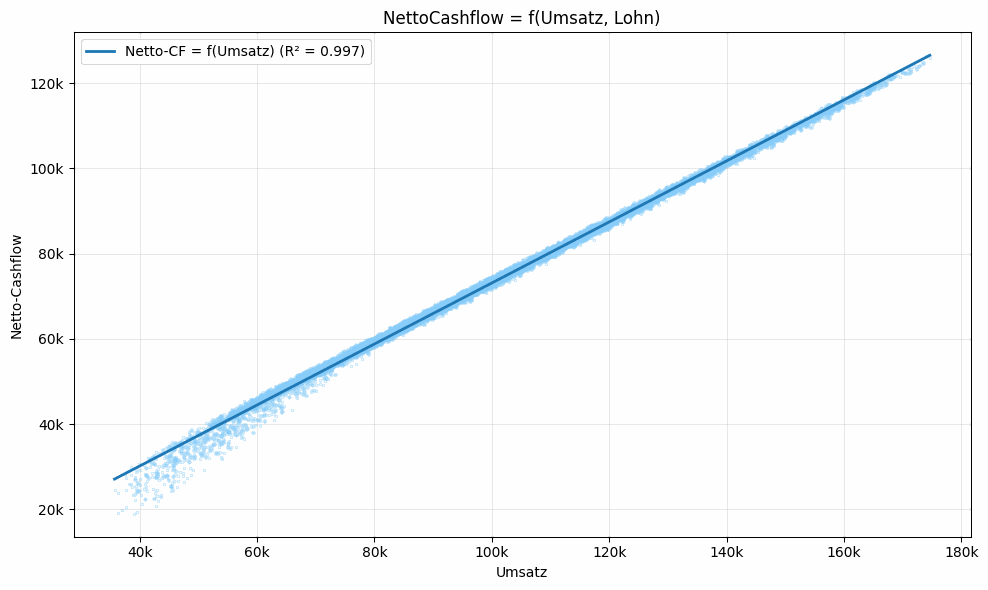
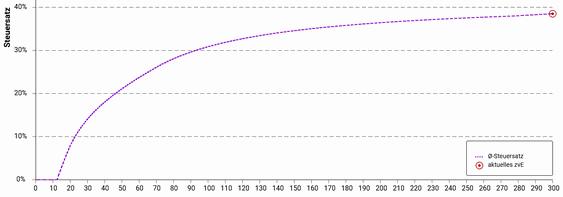
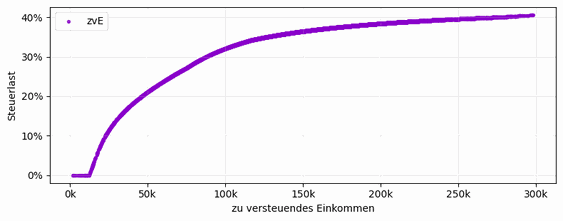
Dieses Ergebnis überrascht zunächst, da die Steuerprogression (Bild 5) eine Optimierung suggeriert. Die Steuerprogression ist auch in der Simulation enthalten (Bild 6). Der verbreitete Denkfehler liegt jedoch in der Interpretation: Verhältniszahlen bilden die relevanten Vorgänge nicht ab. Geld wirkt in absoluten Beträgen. Niedrige Einkommen werden mit niedrigeren Steuerfaktoren multipliziert, höhere Einkommen mit höheren. Höheres Brutto führt daher im Kern zu proportional höherem Netto – der Anstieg ist lediglich durch Steuerabzüge gedämpft. Genau das zeigt Bild 4.

Warum wird dennoch häufig beklagt, dass ein höheres Brutto sogar zu einem geringen Netto führen kann? Auch dieser Effekt tritt in der Simulation auf. Seine Größenordnung ist jedoch begrenzt (Bild 7): Es handelt sich überwiegend um wenige hundert Euro. Für niedrige Einkommen ist das relevant; für das hier betrachtete System ergibt sich daraus jedoch kein nennenswertes Optimierungspotenzial, da Umsätze und Kosten nicht exakt bekannt sind. 

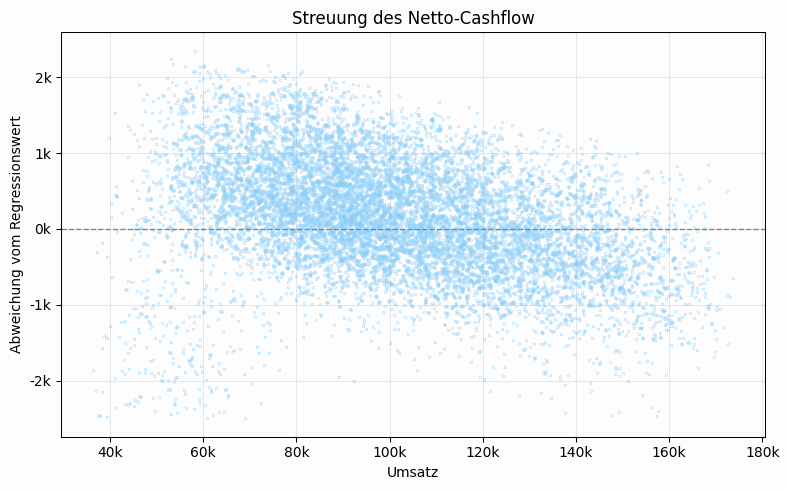
Insgesamt ist die MC schlüssig und erlaubt die Konstruktion einer einfachen Entscheidungsregel.

Durch MDO, IPA und MC wurde eine erhebliche Komplexitätsreduktion erreicht. Die vernetzten Teilsysteme mit ihren jeweiligen Rechenlogiken lassen sich auf ein einfaches Entscheidungsproblem zurückführen: Für den Vermögenszuwachs ist die konkrete Umsatz-Gehalts-Kombination weitgehend unerheblich. Niedrigere Steuerabflüsse im privaten Bereich führen zu höheren Steuerabflüssen im Geschäft und umgekehrt. Eine systemweite Steueroptimierung über das Gehalt ist damit nicht möglich. Es verbleibt nur: Viel Umsatz hilft viel.

Das ursprünglich komplexe Entscheidungsproblem reduziert sich damit auf eine deutlich einfachere Frage: Wie viel CF ist erforderlich, um die Lebenshaltungskosten zu decken? Diese Kosten sind gut bekannt und in der Regel steuerbar. Extreme Sonderfälle werden über die Notgroschen abgefedert.

Diese Einschätzung gilt auch bei langfristiger Betrachtung. Mittels der zufälligen Wachstumsraten im MDO ließen sich Vermögen und Kosten in der MC verzinsen und zeitversetzt auszahlen. Das ändert aber die Schlussfolgerungen nicht, solange der CF die Lebenshaltungskosten deckt, diese auf einem bodenständigen Niveau bleiben und der Vermögensverzehr über die Notgroschen kontrolliert wird. Erforderlich ist lediglich eine regelmäßige Anpassung des Modells an geänderte steuerliche Ansatzvorschriften und veränderte Lebensumstände.

Das gezeigte Vorgehen ist universell einsetzbar. MDO, IPA und MC eignen sich einzeln oder kombiniert für unterschiedliche komplexe Entscheidungsprobleme. In der Produktentwicklung würden die Kopplungsvariablen beispielsweise auf physikalischen Zusammenhängen oder auf Signal- und Datenflüssen beruhen. In der Praxis führen die Fachbereiche ihre jeweiligen MCs durch und geben die resultierenden Kopplungsvariablen an das SE oder andere Fachbereiche weiter. So wird iterativ zusammengearbeitet, bis die systemweite Zielfunktion(en) des NLP konvergiert.

— Ihr, Nico Litschke

1. ↑ Dörner, D. (2002). Die Logik des Mißlingens: Strategisches Denken in komplexen Situationen (15. Aufl.). Reinbek bei Hamburg: Rowohlt.
2. ↑ Agte, J., de Weck, O., Sobieszczanski-Sobieski, J., Arendsen, P., Morris, A., & Spieck, M. (2009). MDO: Assessment and direction for advancement—An opinion of one international group. Structural and Multidisciplinary Optimization, 40(1–6), 17–33. https://doi.org/10.1007/s00158-009-0381-5
3. ↑ de Weck, O. L., & Jones, M. B. (2006). Isoperformance: Analysis and design of complex systems with desired outcomes. Systems Engineering, 9(1), 45–61. https://doi.org/10.1002/sys.20043
4. ↑ Bundesministerium der Finanzen (BMF). (2026). Berechnungen und Informationen zur Einkommensteuer. https://www.bmf-steuerrechner.de/ekst/eingabeformekst.xhtml